Constituency Trees
 | |
| Lecture video: |
web TODO Youtube |
|---|---|
{{#ev:youtube|https://www.youtube.com/watch?v=y_9SEdG1u3U%7C800%7Ccenter}}
Context Free Grammar
Grammars, generally, are a way of describing a potentially infinite set of strings (sentences) using a finite set of production rules. In a context-free grammar, production rules take the following form:
V → w
V is a non-terminal symbol (for natural languages, non-terminals usually correspond to phrases, such as NP for noun phrases) and w is a (non-empty) string of terminals (words) and nonterminals. It is known that CFGs cannot fully describe natural languages but for MT, they can serve as a very useful simplification.
One nonterminal symbol serves as the top-level nonterminal where the generation starts (or where analysis ends) -- for natural languages, we usually use the symbol S (sentence).
The following example grammar can generate (or analyze) sentences such as Dogs sleep (grammatical English) or The black cat sleep (ungrammatical).
S -> NP VP NP -> dogs VP -> sleep NP -> Det Adj N Det -> the Adj -> black N -> cat
We can mend this grammar by dividing each nonterminal into two variants -- one for singular and one for plural. In general, linguistic phrases have many independent linguistic properties which would require us to split the nonterminals into an exponential number of variants.
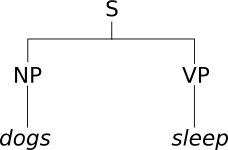
When a natural language sentence is analyzed with a constituency grammar, we obtain a parse tree, such as the following:
Syntax in Machine Translation
In MT, constituency trees can be used either on the source side, on the target side or both.