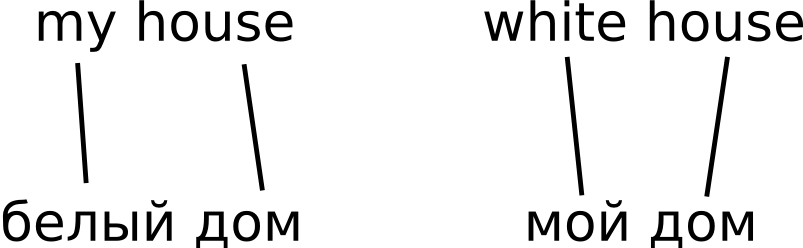Word Alignment: Difference between revisions
No edit summary |
No edit summary |
||
| Line 22: | Line 22: | ||
The so-called IBM models<ref name="ibmmodels">Peter F. Brown, Stephen A. Della Pietra, Vincent J. Della Pietra, Robert L. Mercer ''[http://www.aclweb.org/anthology/J93-2003 The Mathematics of Statistical Machine Translation: Parameter Estimation]''</ref> are the best-known and still the most commonly used approach to word alignment. In our lecture, we only go through the first, simplest model. | The so-called IBM models<ref name="ibmmodels">Peter F. Brown, Stephen A. Della Pietra, Vincent J. Della Pietra, Robert L. Mercer ''[http://www.aclweb.org/anthology/J93-2003 The Mathematics of Statistical Machine Translation: Parameter Estimation]''</ref> are the best-known and still the most commonly used approach to word alignment. In our lecture, we only go through the first, simplest model. | ||
The algorithm for IBM-1 only looks at ''lexical translation probability''. So basically, our goal is to fill in a matrix which says for each target word <math>w_t</math> and source word <math>w_s</math> what is the probability <math>P(w_t|w_s)</math>. Once we have this dictionary, we can get the actual alignments by finding the most probable target word for each source word (just in the case of IBM-1) and drawing a link there. | |||
The learning algorithm is an instance of [http://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm Expectation-maximization]. In general, this is an iterative procedure which alternates between two steps until convergence: | |||
# '''E-step''': apply current model parameters to the data | |||
# '''M-step''': estimate new model parameters from the data | |||
Initially, all of our translation probabilities are uniform. | |||
=== Model Limitations === | === Model Limitations === | ||
Revision as of 16:22, 24 March 2015
 | |
| Lecture video: |
web TODO Youtube |
|---|---|
| Exercises: | IBM-1 Alignment Model |
In the previous lecture, we saw how to find sentences in parallel data which correspond to each other. Now we move one step further and look for words which correspond to each other in our parallel sentences.
This task is usually called word alignment. Note that once we have solved it, we get a (probabilistic) translation dictionary for free. See our sample "parallel corpus":
For example, if we look for translations of the Russian word "дом", we simply collect all its alignment links (lines leading from the word "дом") in our data and estimate translation probabilities from them. In our tiny example, we get P("house"|"дом") = 2/2 = 1.
IBM Model 1
The so-called IBM models[1] are the best-known and still the most commonly used approach to word alignment. In our lecture, we only go through the first, simplest model.
The algorithm for IBM-1 only looks at lexical translation probability. So basically, our goal is to fill in a matrix which says for each target word and source word what is the probability . Once we have this dictionary, we can get the actual alignments by finding the most probable target word for each source word (just in the case of IBM-1) and drawing a link there.
The learning algorithm is an instance of Expectation-maximization. In general, this is an iterative procedure which alternates between two steps until convergence:
- E-step: apply current model parameters to the data
- M-step: estimate new model parameters from the data
Initially, all of our translation probabilities are uniform.
Model Limitations
IBM Model 1 only looks at lexical translation probability. It has no notion of word position so it is happy to align two neighboring words in the source sentence to two completely different positions in the target. It also disregards how many alignment links lead to a particular word (it does not model the so-called word fertility), so in some cases, it can even align the whole source sentence to a single target-side word, leaving other target words unaligned. Higher IBM models address these limitations with probability estimates of distortion and fertility.
Exercises
References
- ↑ Peter F. Brown, Stephen A. Della Pietra, Vincent J. Della Pietra, Robert L. Mercer The Mathematics of Statistical Machine Translation: Parameter Estimation