Constituency Trees: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 27: | Line 27: | ||
Adj -> black | Adj -> black | ||
N -> cat | N -> cat | ||
We can mend this grammar by dividing each nonterminal into two variants -- one for singular and one for plural. In general, linguistic phrases have many independent linguistic properties which would require us to split the nonterminals into an exponential number of variants. | |||
When a natural language sentence is analyzed with a constituency grammar, we obtain a parse tree, such as the following: | When a natural language sentence is analyzed with a constituency grammar, we obtain a parse tree, such as the following: | ||
| Line 32: | Line 34: | ||
[[File:dogs-sleep.png|200px]] | [[File:dogs-sleep.png|200px]] | ||
In MT, constituency trees can be used either on the source side (tree-to-string MT), on the target side (string-to-tree) or both (tree-to-tree). | |||
== | == Tree-to-Tree Translation == | ||
We describe the scenario where phrase-structure trees are used on both sides. In that case, translation can be viewed as parsing of the source sentence using a '''synchronous CFG'''. Such a grammar contains production rules with two right-hand sides: one for the source side and one for the target side. | |||
Consequently, the constituency tree of the translation is constructed as the source sentence is parsed. The translation can then simply be read off the parse tree. | |||
Latest revision as of 14:01, 12 August 2015
 | |
| Lecture video: |
web TODO Youtube |
|---|---|
Context Free Grammar
Grammars, generally, are a way of describing a potentially infinite set of strings (sentences) using a finite set of production rules. In a context-free grammar, production rules take the following form:
V → w
V is a non-terminal symbol (for natural languages, non-terminals usually correspond to phrases, such as NP for noun phrases) and w is a (non-empty) string of terminals (words) and nonterminals. It is known that CFGs cannot fully describe natural languages but for MT, they can serve as a very useful simplification.
One nonterminal symbol serves as the top-level nonterminal where the generation starts (or where analysis ends) -- for natural languages, we usually use the symbol S (sentence).
The following example grammar can generate (or analyze) sentences such as Dogs sleep (grammatical English) or The black cat sleep (ungrammatical).
S -> NP VP NP -> dogs VP -> sleep NP -> Det Adj N Det -> the Adj -> black N -> cat
We can mend this grammar by dividing each nonterminal into two variants -- one for singular and one for plural. In general, linguistic phrases have many independent linguistic properties which would require us to split the nonterminals into an exponential number of variants.
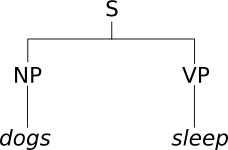
When a natural language sentence is analyzed with a constituency grammar, we obtain a parse tree, such as the following:
In MT, constituency trees can be used either on the source side (tree-to-string MT), on the target side (string-to-tree) or both (tree-to-tree).
Tree-to-Tree Translation
We describe the scenario where phrase-structure trees are used on both sides. In that case, translation can be viewed as parsing of the source sentence using a synchronous CFG. Such a grammar contains production rules with two right-hand sides: one for the source side and one for the target side.
Consequently, the constituency tree of the translation is constructed as the source sentence is parsed. The translation can then simply be read off the parse tree.